This week, I had the pleasure of returning to BasisTech’s lovely office in Boston to give an invited talk on the role of active learning in today’s LLM-based machine learning landscape.

In summary: Even in the era of large language models, active learning remains a powerful technique to reduce training costs. However, it is also the case that some ingenuity may be required in order to achieve these advantages. Traditional applications of active learning often assume that uncertainty is relatively easy to gauge, but the paper discussed in this talk demonstrates that this is not necessarily the case for LLMs.

This talk comes at a particularly interesting time, since AI has recently gone from requiring bespoke solutions for every problem to something which can be easily adapted through clever prompt engineering.

Even still, practice shows us that getting optimal performance out of your language model often requires doing some amount of fine-tuning; that is, collecting additional training data which is used to tweak the internal weights of the model.

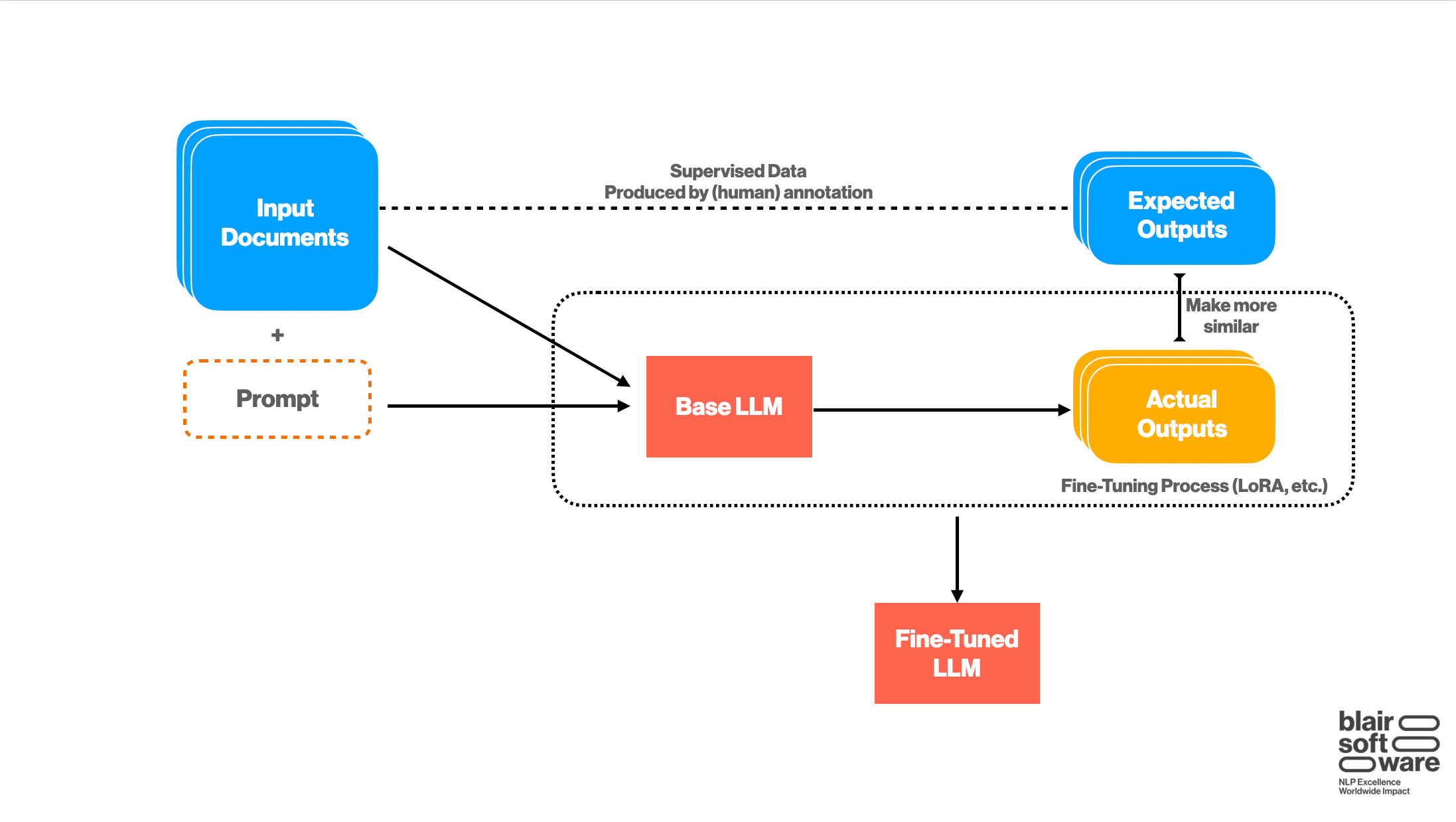
While techniques such as Low-Rank Adaptation (LoRA) make the fine-tuning process itself rather straightforward, the real challenge tends to be the collection of training data needed. In particular, there are two problems:

First, data is expensive. A high-quality data annotation project can easily cost thousands once factoring in the iteration on the annotation guidelines, the process of adjudicating conflicting annotations, and, of course, renumerating the data annotators themselves. In specialized domains such as law or medicine, these costs further rise, easily surpassing $10,000.

Second, while the fine-tuning process is relatively easy to run, that does not necessarily mean that it is cheap. In particular, the cost of fine-tuning is a function of the amount of data being used to train.

We can ask ourselves: how much data do we need in order to train a model that is good enough?

This is where active learning comes in.

What is Active Learning?

To set the stage, let’s think about a simple machine learning problem: binary classification of points in 2D space:

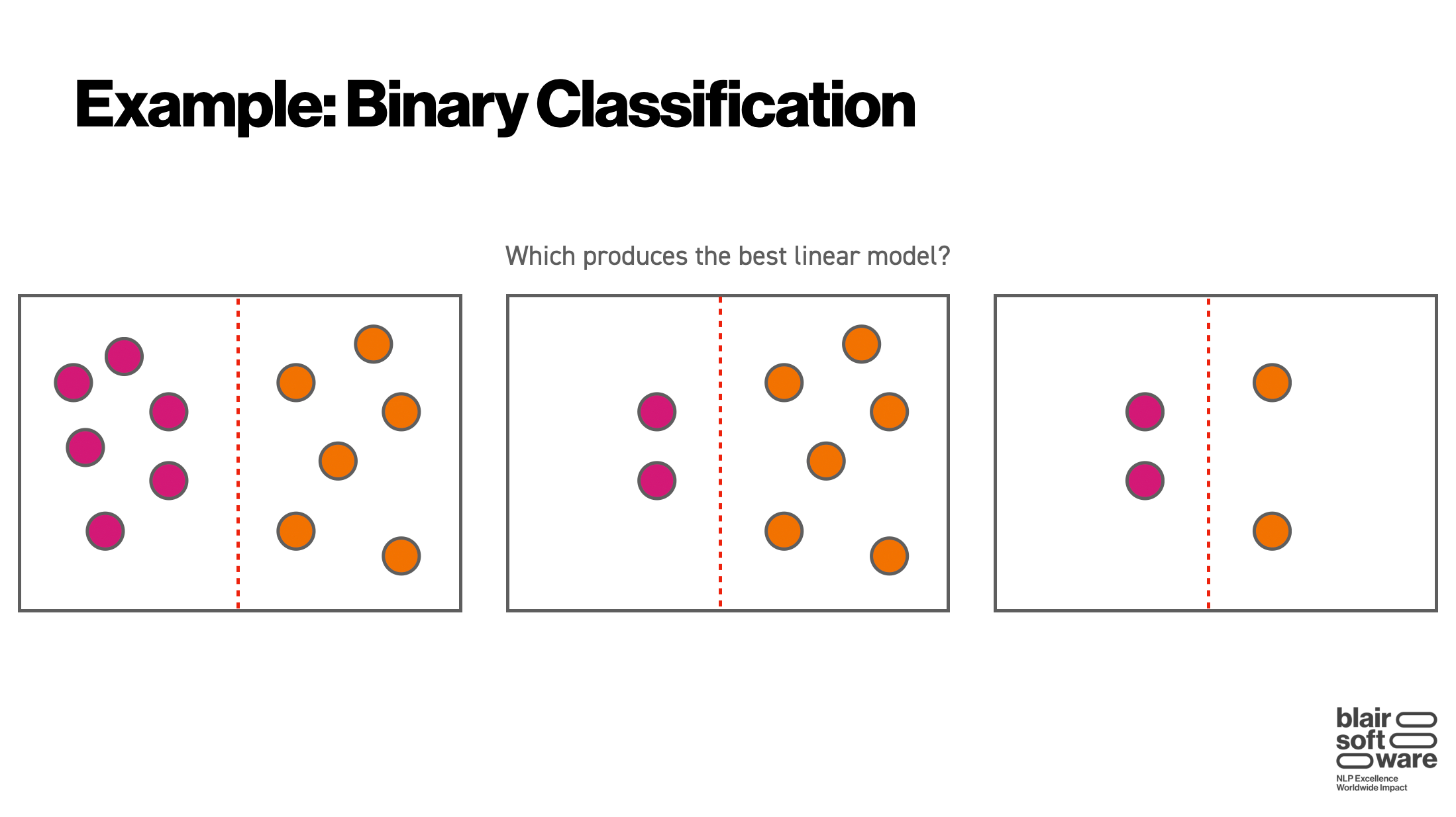
In this scenario, our goal is to draw a line which separates the two colors. Looking at the above diagram, we see that no matter which dataset we use, we end up with the same line (for those of you who have studied machine learning, you may recognize that the dataset on the right exclusively consists of the support vectors). Thus, if we have some training cost involved which scales with our dataset size, we would ideally like to use the smallest dataset (on the right) to train our model.

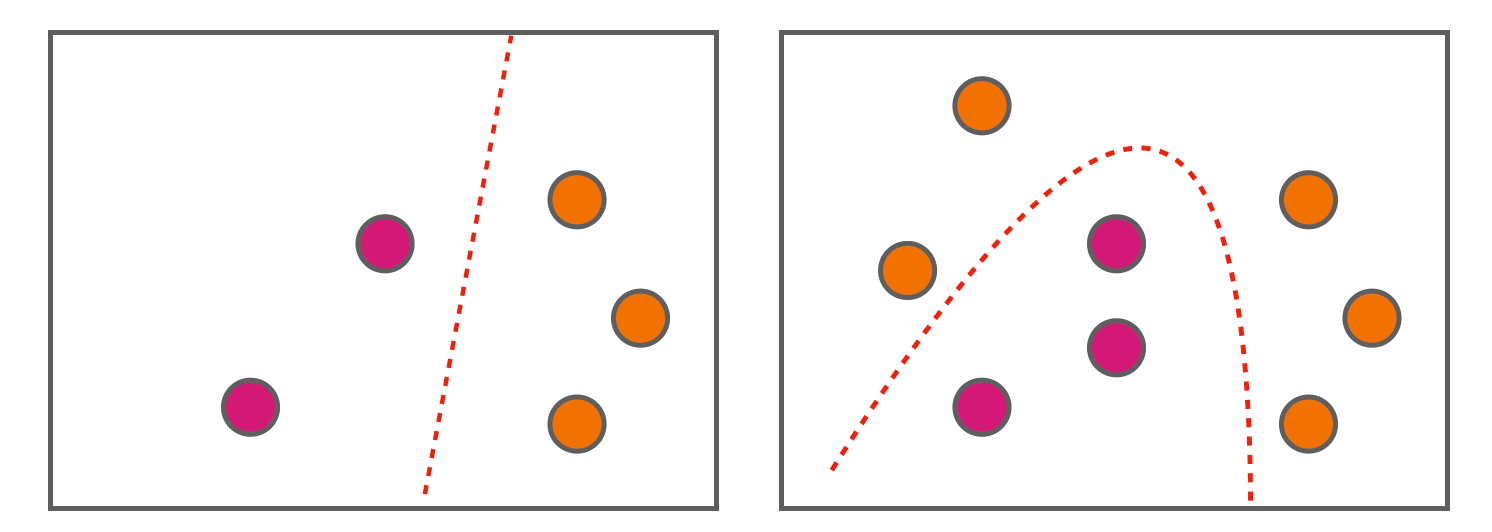
The issue is that we don’t know what this minimal dataset exactly looks like until we have labeled everything. As shown below, sometimes you really need to label everything to get the full picture:

Now, before discussing active learning, one final concept we need to understand is online machine learning. This is simply a paradigm in which we iteratively retrain and update our model as new information is discovered:

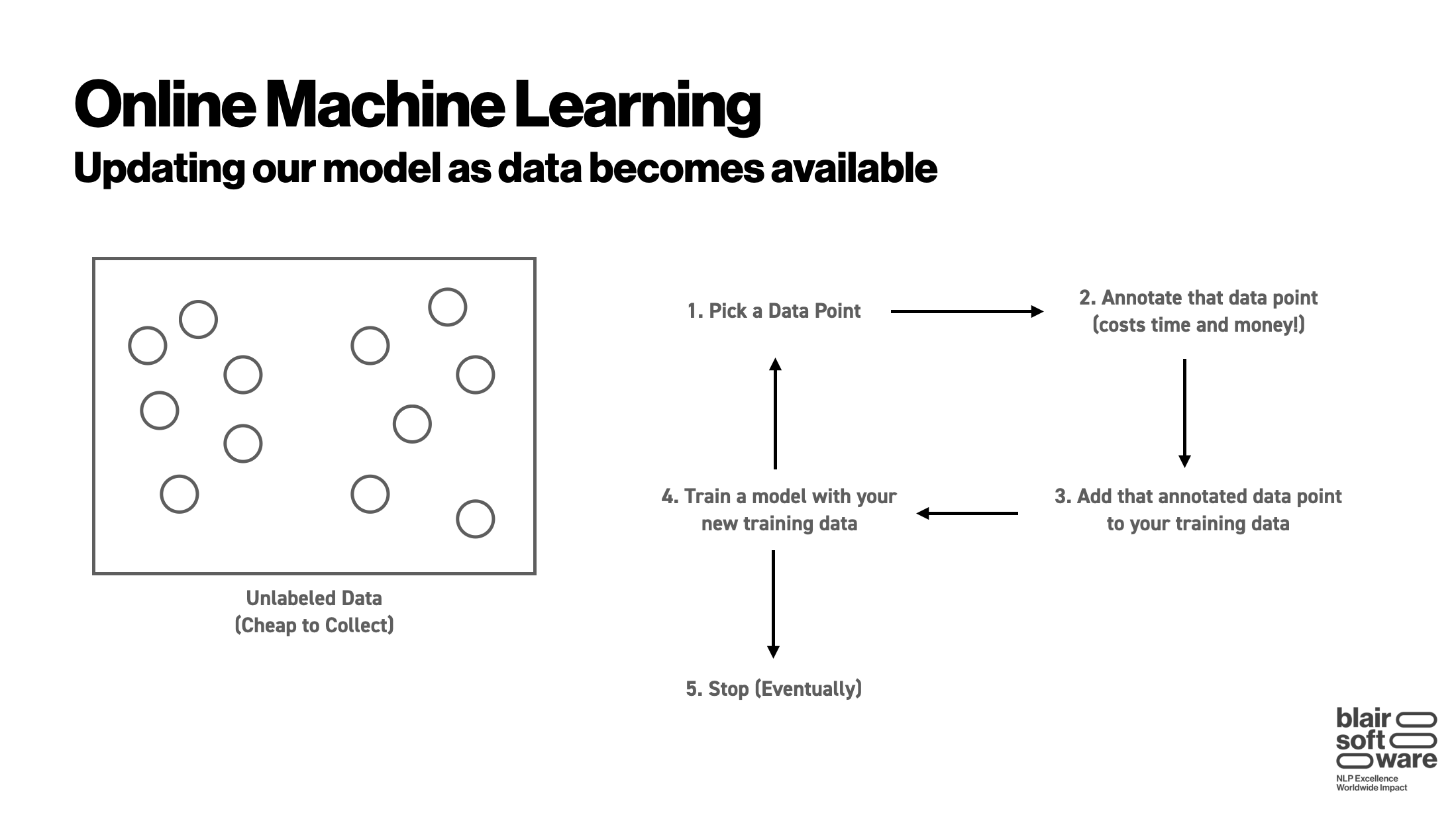
Here, we assume that the process of collecting unlabeled data is relatively cheap (which is typical in many situations). We likewise assume that there is some sort of annotator who can take an unlabeled data point and provide a label (in the case of our binary classification, a color) for it. We then repeatedly do the following:

1. Select a data point
2. Annotate that data point
3. Add that annotated data point to our model training dataset
4. Retrain our model with the new dataset
5. When finished, stop.

Now, there are two key snags with this algorithm: deciding which point to pick during step 1 and deciding what “finished” means on step 5. Active learning gives us the answer to both of these questions.

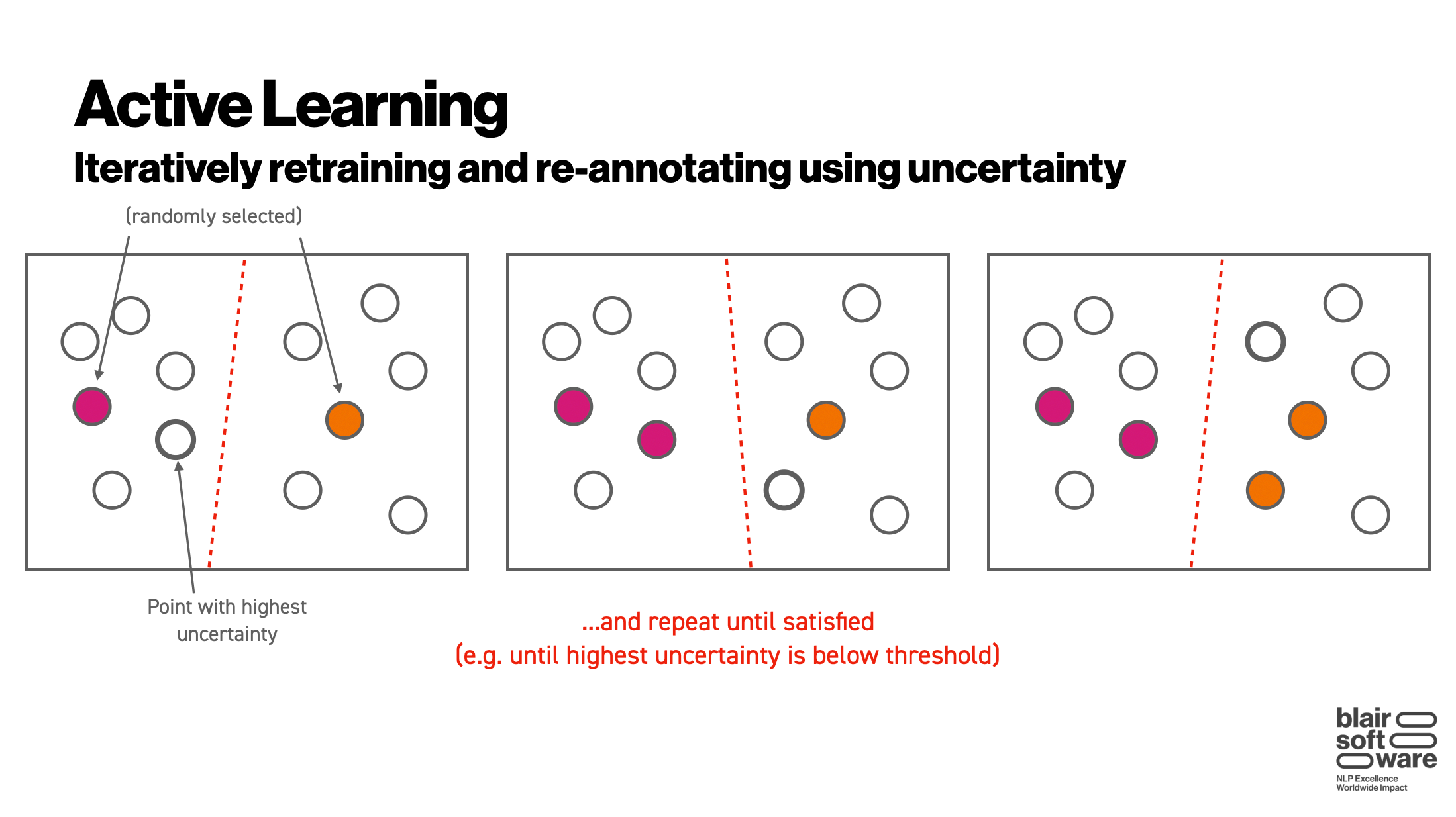
The key trick of active learning is to let the data answer the above questions. Specifically, we pick a couple of random points, train a model with those points, and then use the uncertainty of that model (in our binary classifier example, this would be inversely related to the distance between an unlabeled data point and the current separation line) to select which data point we should annotate next. The thinking goes that, once the highest uncertainty level drops beneath some certain threshold, we should have arrived at a decent approximation for what the optimal subset of training data actually is:

What does this have to do with LLMs?

In order to think about applying active learning to large language models, we need to scale up from our simple binary classification example. Let’s think about how LLMs predict text. To a user of a website like ChatGPT, it might look something like the following:

Under the hood, though, something more complicated is happening: for each of these tokens¹ returned by the model, the model is actually producing a probability distribution over all possible tokens that could be returned. This distribution is then decoded (usually via sampling) into a choice of which token is to be returned:

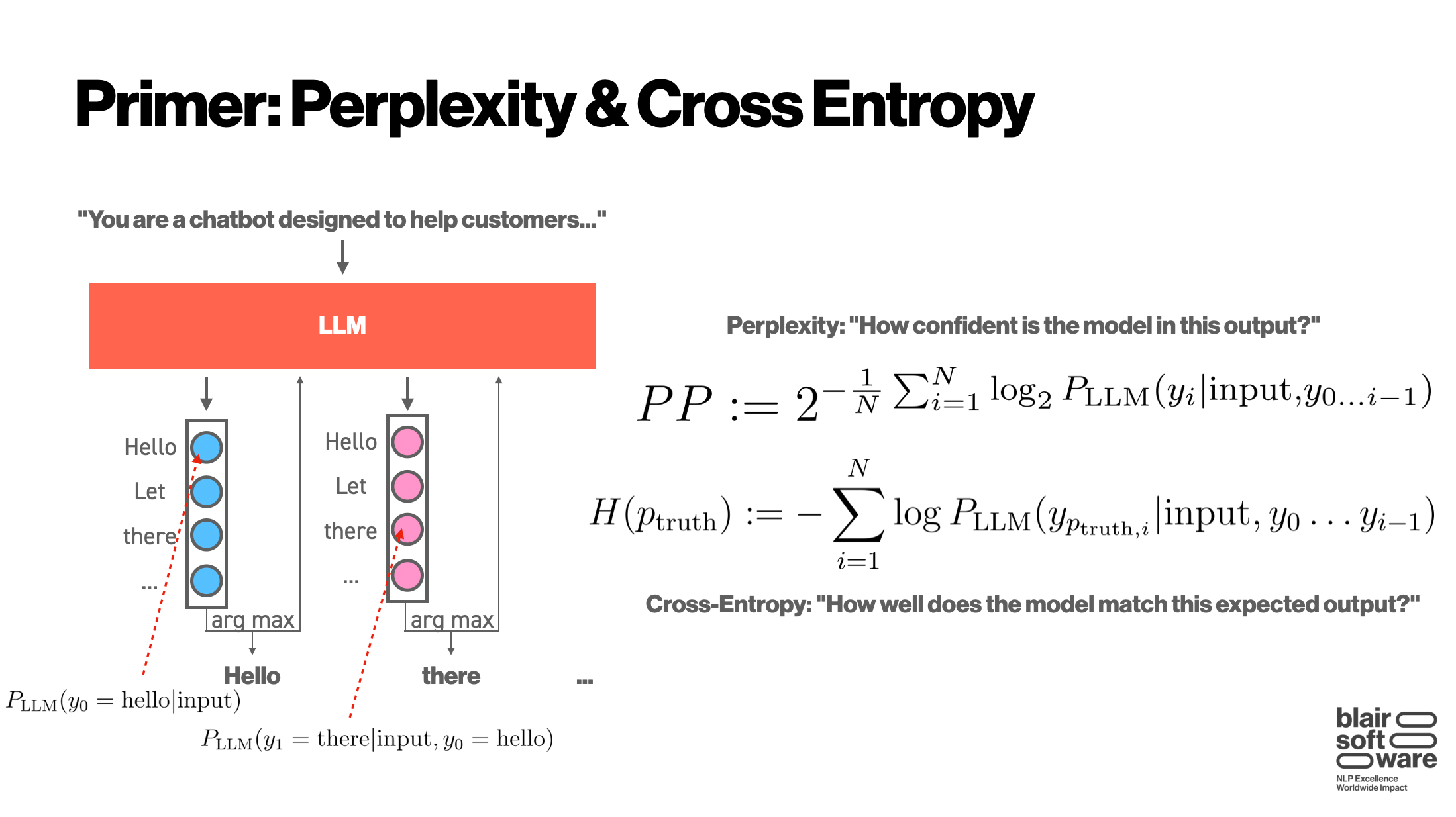
The advantage of looking at these probability distributions is that we can define a couple of measures, shown above. The perplexity allows us to assign a score to how confident a model is in its outputs. If the top-scoring token has a low probability (as assigned by the model), then we say the model has a higher perplexity (i.e. is more confused) on that input. Similarly, cross-entropy allows us to take an expected reply and check how well it aligns with what the model wanted to reply.

So, let’s take a look at a specific model: Flan-T5. This model comes from the seminal on multi-instruction tuning, in which an LLM was trained to follow instructions across many different tasks, as illustrated in the Flan-T5 paper:

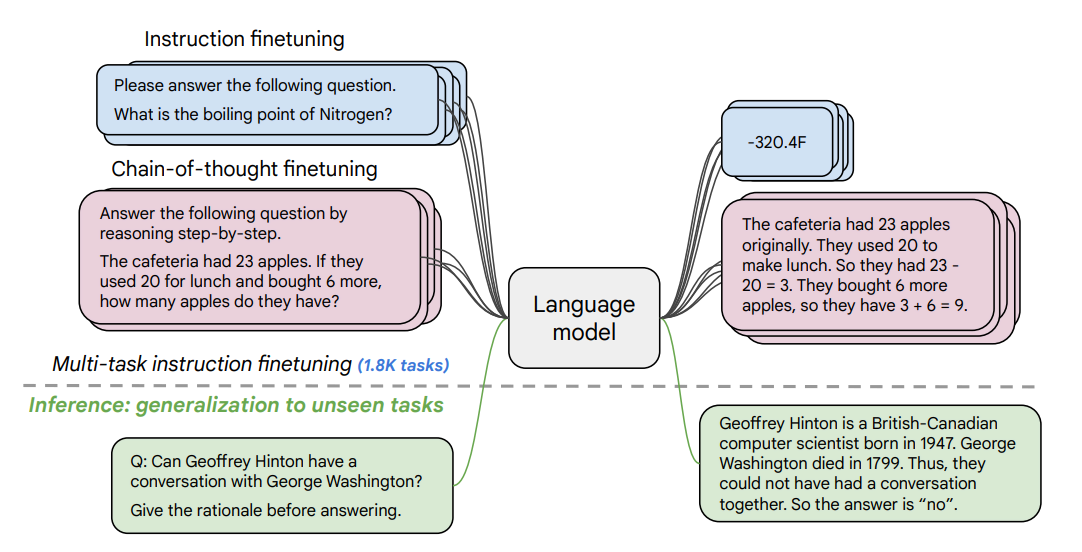
This technique showed immense promise, with performance increasing more and more as additional tasks were added to the training set. The issue, however, is that the compute costs incurred for each additional task were enormous. Thus, some readers of this paper asked themselves: can we select an optimal set of tasks for doing multi-instruction tuning? Upon reflection, this is very similar to the problem setup in active learning, and so the 2023 paper “Active Instruction Tuning: Improving Cross-Task Generalization by Training on Prompt Sensitive Tasks” by Kung et al was born. In this paper, they reformulate this question into an active learning problem, with the use of a novel metric known as prompt uncertainty:

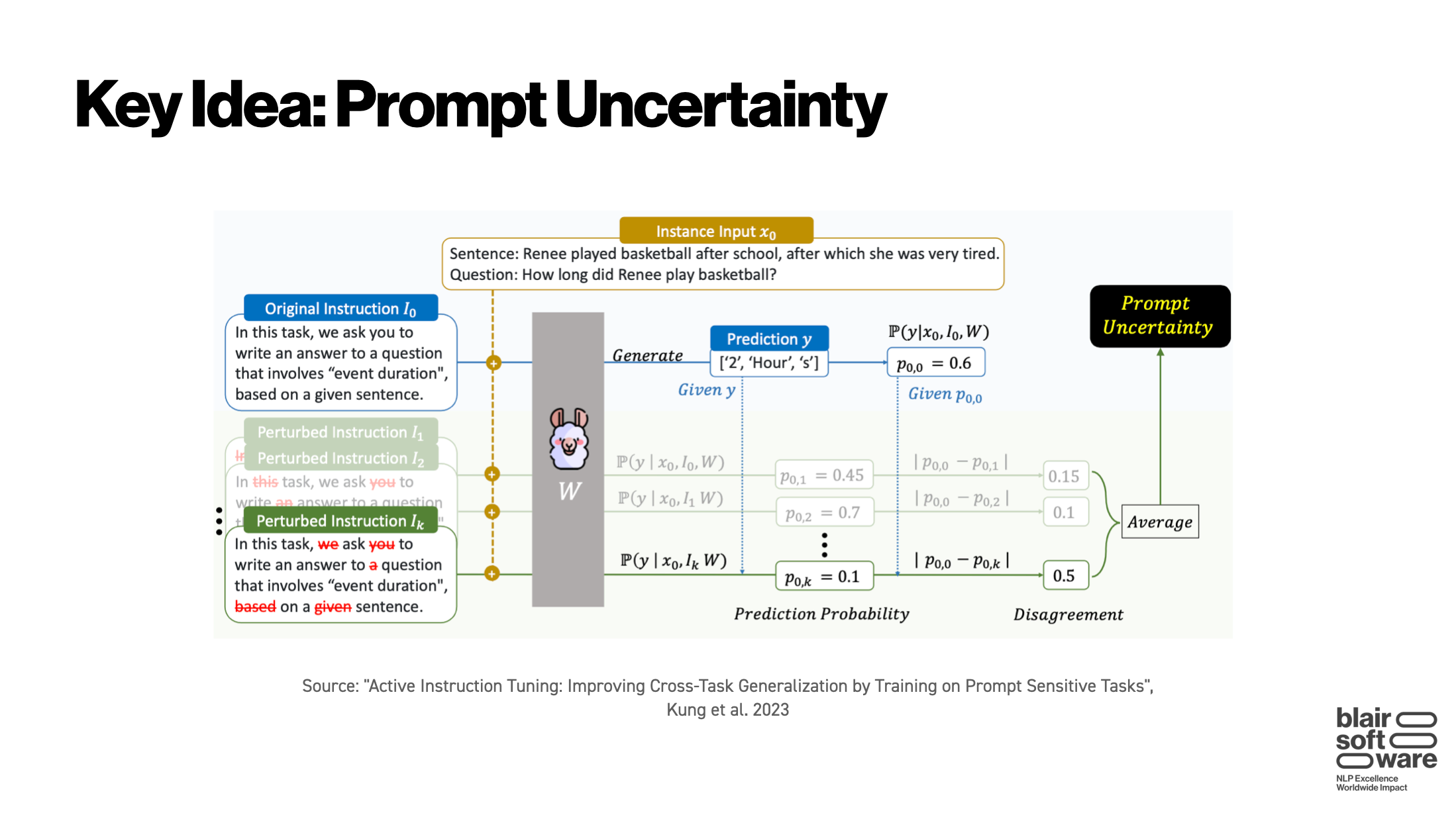
Prompt uncertainty is defined by taking an input for a task and slightly randomly corrupting it (the “perturbed instructions” on the left). Then, the original instruction and the perturbed instructions are each run through the model separately. We can then check how the probability distributions of the model’s outputs compare between the original and new inputs. The idea behind prompt uncertainty is that the probabilties should have changed a lot for tasks which the model understands less, and so we measure this change.

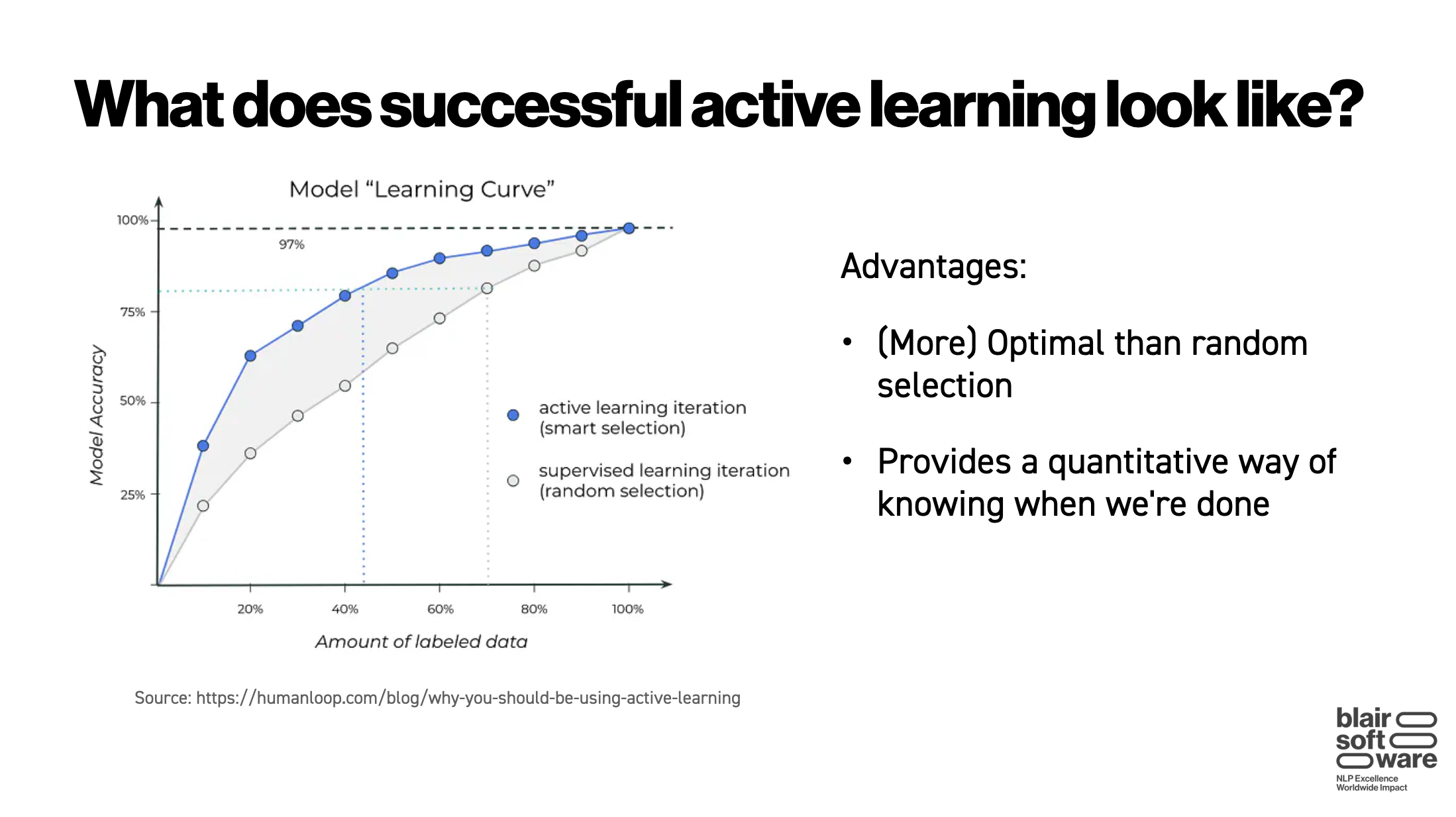
How well does it work? Quite well, actually:

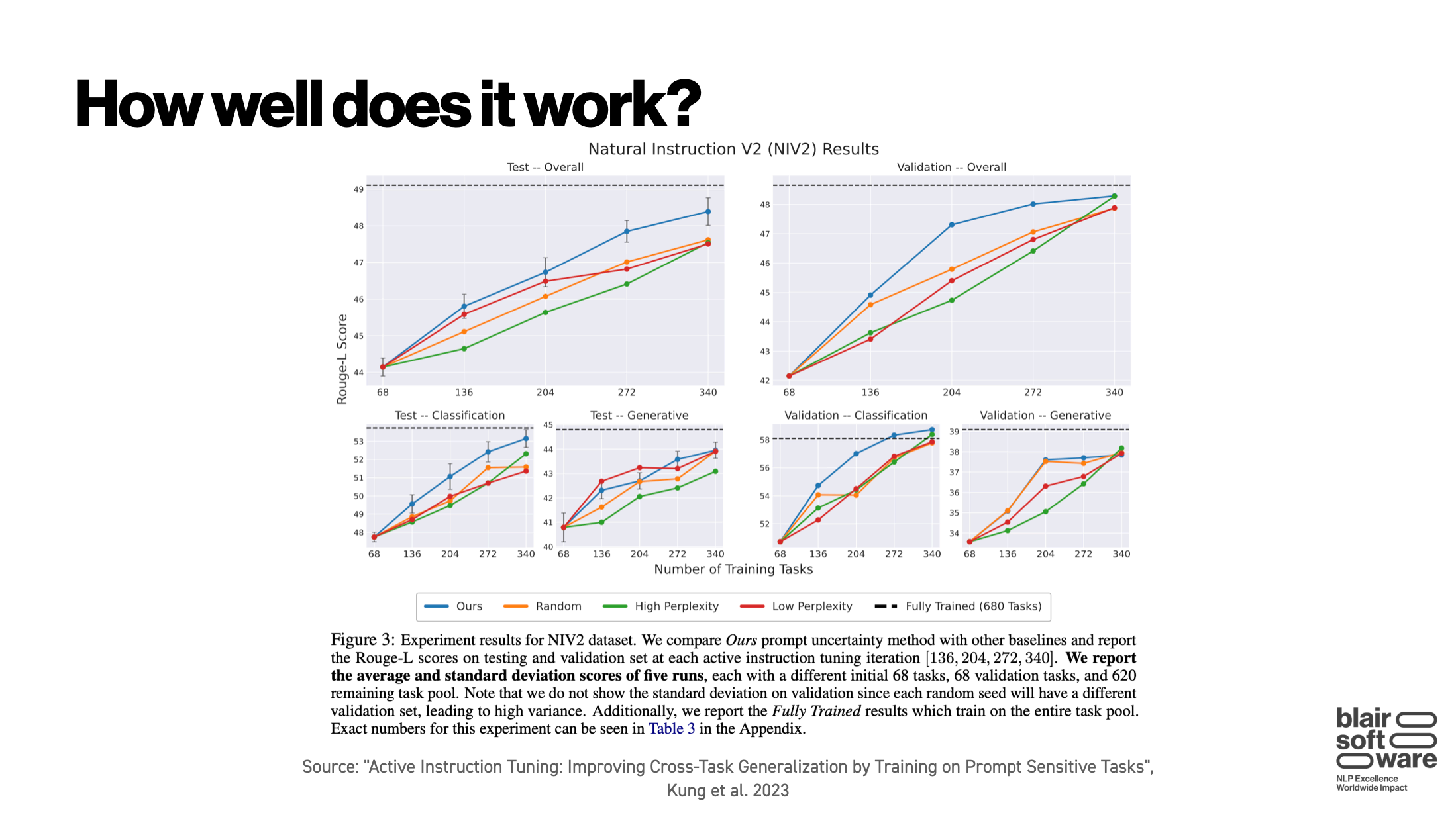
Compare the blue and orange lines, and notice the similarity to the above diagram showing what active learning should ideally look like. Another strong result from the paper was that the authors’ prompt uncertainty metric appears to give a better guide of what will help model performance than just looking at the model perplexity (which is often done in active learning for other NLP tasks).

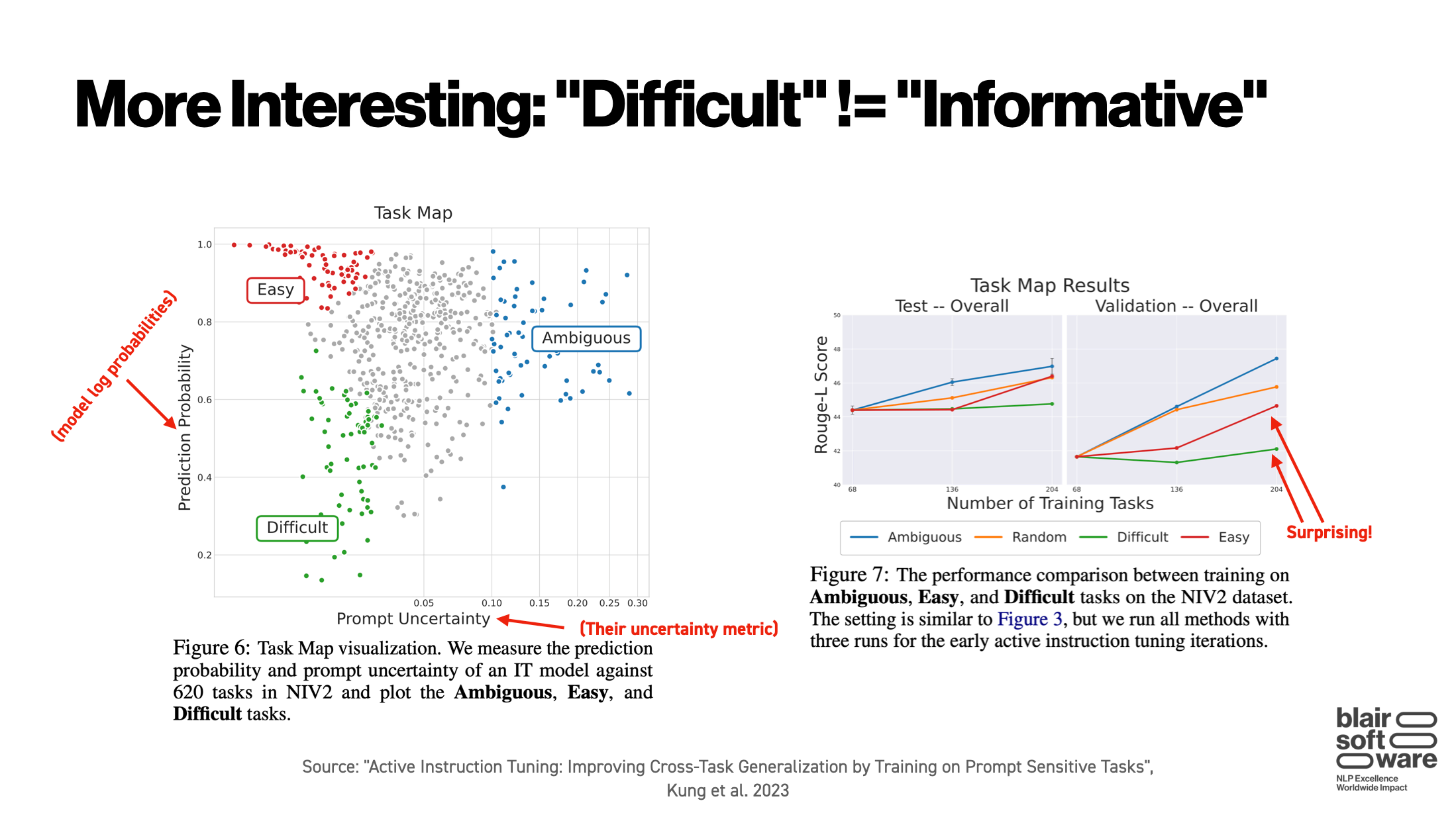
What is the reason for this disconnect? The authors speculate:

We hypothesize that Difficult tasks can be too specific and hard to learn, therefore useless for improving the [Instruction Tuning] model’s cross-task generalization.

Nonetheless, this work clearly demonstrates active learning’s continued potential for cost-savings. There are a couple of interesting follow-up directions to this work:

1. Can we generalize the intuition that led to prompt uncertainty to other fine-tuning tasks?
2. On the flipside, can prompt uncertainty be effectively used for a single task?

These questions, like many others, are worth exploring!